The analogy between the decomposition of the square in the plane and the cube in space gave us a way to find the volume formula for an off-center pyramid with a square base. A square is divided into two congruent triangles by a diagonal, and so is a rectangular region. The formula for the volume of prisms can also be applied to the volume of pyramids, which occupy only one third of the space of a corresponding prism with the same base and height. To calculate the volume of a pyramid, we simply multiply the area of the one of the bases times one third of the height of the pyramid.
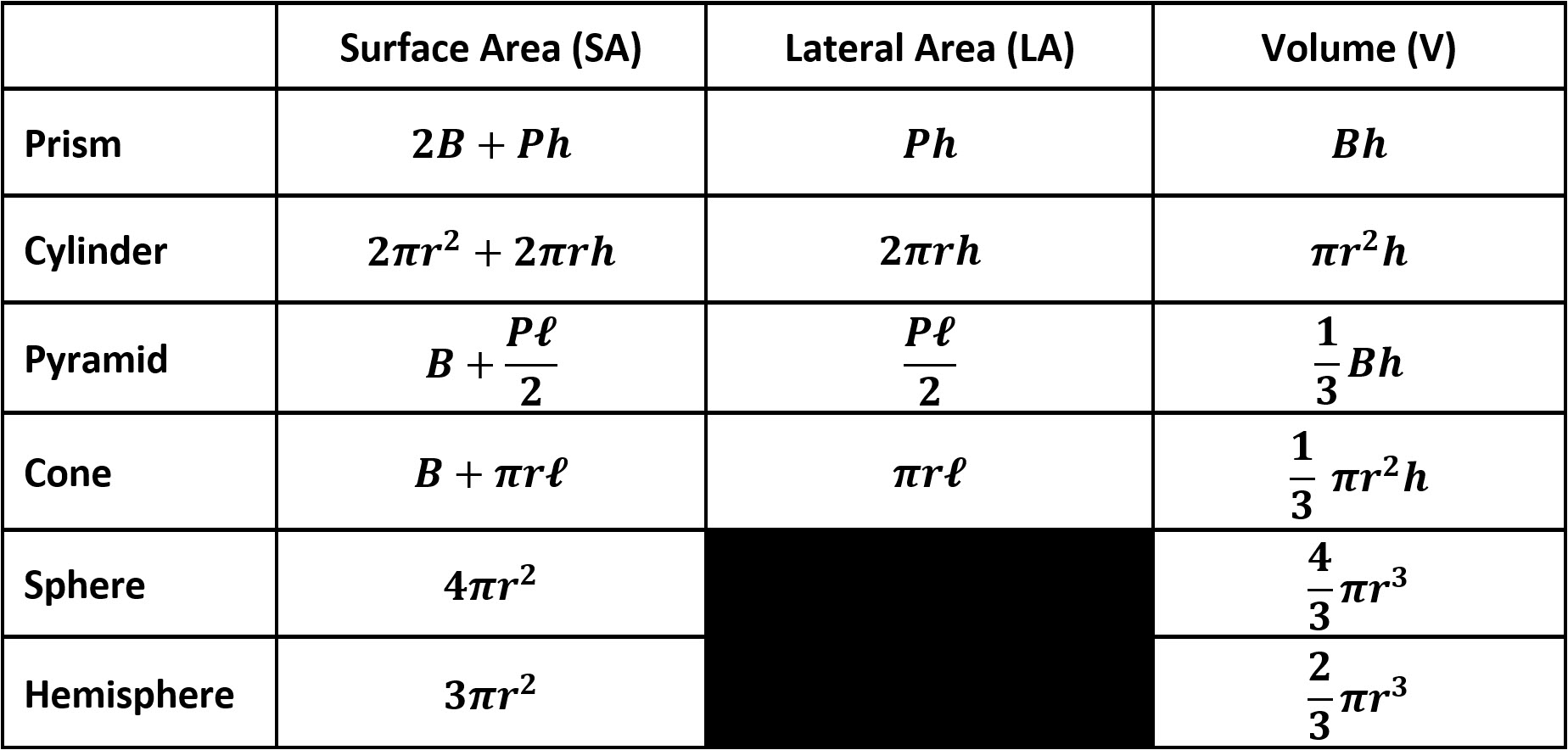
This formula is very similar to volume of cylinder and volume of cone formulas. From the earlier section, we have learned that the volume of a pyramid is (1/3) × × . The volume of pyramid is space occupied by it it is defined as the number of unit cubes that can be fit into it. A pyramid is a polyhedron as its faces are made up of polygons. All the side faces of a pyramid are triangles where one side of each triangle merges with a side of the base.
Let us explore more about the volume of pyramid along with its formula, proof, and a few solved examples. The formulas for volumes of various kinds of square-based pyramids can be modified to give formulas for pyramids formed by cutting off a corner of a cube. The dimension of the space again appears in the denominator of the formula, but in a new way. Cutting off one corner of a square produces a triangle with half the area.
Cutting off one corner of a cube produces a pyramid with a triangular base. We can obtain this same triangular pyramid by decomposing a square-based pyramid into four pieces. If we approximate the square-based pyramid by a stack of square slabs, then the triangular pyramid is approximated by a stack of triangular slabs each with half the volume. In general then-dimensional volume of a corner figure of an n-cube will be 1/n! Stands for "n factorial," obtained by, multiplying together the first n numbers.
We begin with a cube, having three times the, volume of an off-center pyramid contained within it. We double the length of one of the edges of the cube to form a rectangular prism, silnultaneously forming an off-center pyramid with the same rectangular base. As we double the length of the edge of the prism, its volume doubles. But all the slabs approximating the volume of the off-center pyramid also double, so the pyramid still has a volume one-third the volume of the prism.
Given any two dimensional shape, we can approximate it arbitrarily closely with a grid of squares, then make square based pyramids on each of those squares up to a common apex. The total volume is the sum of the volumes of the pyramids, which works out the same as #1/3# of the height multiplied by the sum of the areas of the squares. Since the squares approximate the area of the original shape, the volume approximated by the pyramids approximates the volume of a pyramid based on the original shape.
The relationship between volumes of prisms and volumes of pyramids is analogous to the relationship between areas of rectangles and areas of triangles in the plane. A diagonal line divides a square into two congruent isosceles right triangles. More generally, the area of a rectangle is the length of the base multiplied by the height, and the area of a triangle is one-half the length of the base multiplied by the height.
The pattern lies in the denominatior of the fraction. Very similar to the relationship of cones and cylinders. So if you have a pyramid or a cone, you're going to have one third base area times height.
Now the difference between a cone and a pyramid, is that with the cone we could say this base area will always be pi r squared. However, in calculating the volume of the pyramid, you have to ask yourself what type of polygon is the base? So if you had a regular hexagon, for this base area you're going to say one third, apothem times side length times the number of sides divided by 2 times your height. So you have to be careful about what you use for your base area formula. A pyramid is a regular pyramid if its base is a regular polygon and the triangular faces are all congruent isosceles triangles. The volume of a pyramid refers to the space enclosed between its faces.
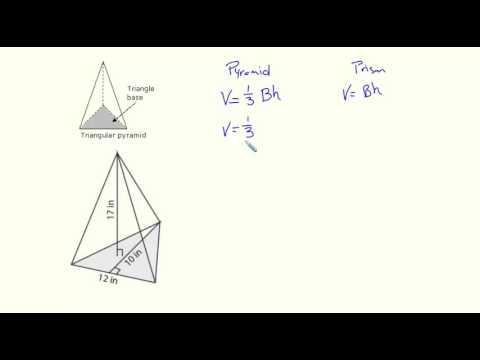
Take a rectangular pyramid full of sand and take an empty rectangular prism whose base and height are as same as that of the pyramid. Pour the sand from the pyramid into the prism, we can see that the prism is exactly one-third full. This formula works because you are adding the base area to the area of all three slanted faces.
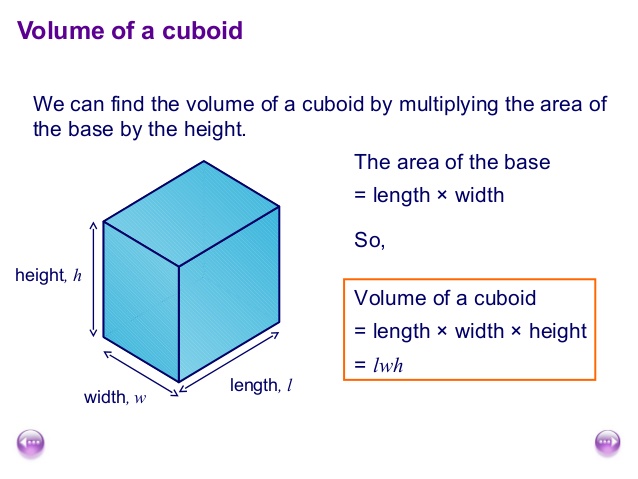
You multiply that sum times the slant height of the triangular pyramid as though you had one big rectangle, and then you take one-half of that as the area of the three triangles. Volume is a measure of capacity and is measure in cubic units. To calculate the volume of a rectangular prism, multiply the area of the base (length × width) times height. We learned how to find the volume of prisms, pyramids, cylinders, and cones.
The relationship between the volumes of pyramids and prisms is that when a prism and pyramid have the same base and height, the volume of the pyramid is 1/3 of the volume of the prism. The volume inside the space of pyramids, prisms, cones, and cylinders can be calculated using specialized formulas. Learn how length, width, and height are used to calculate the volume using formulas for these four objects.
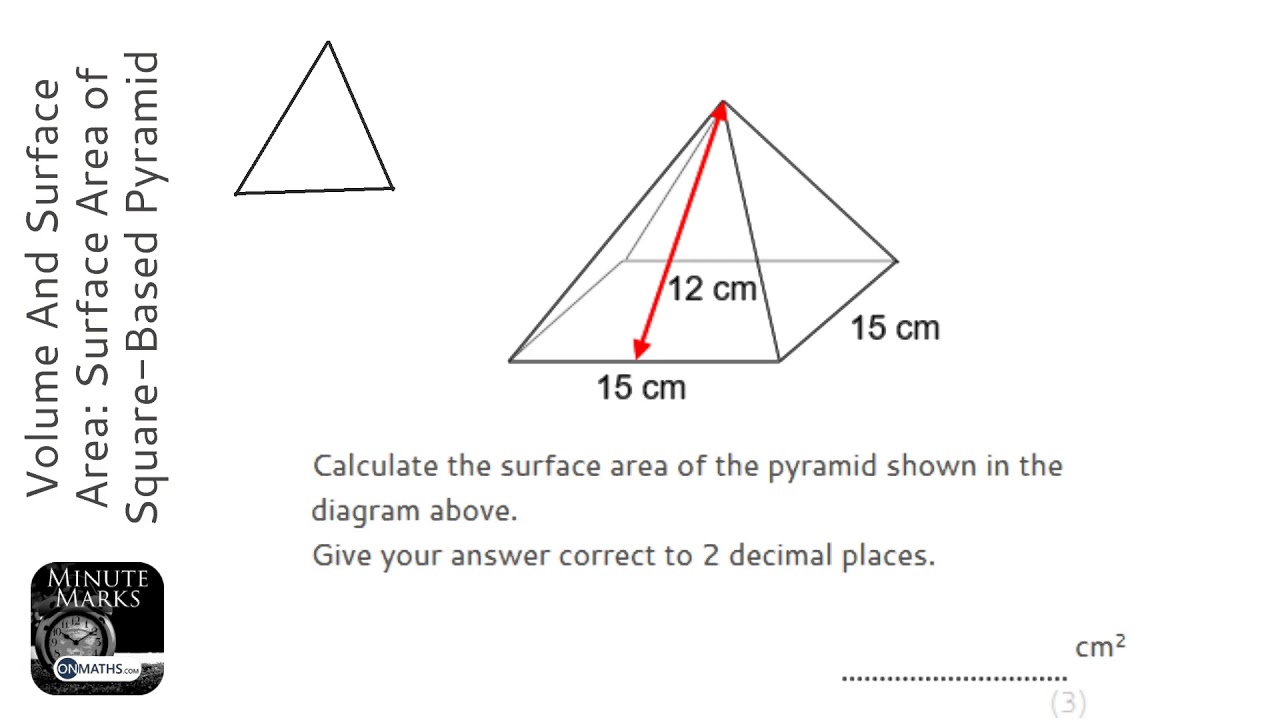
Pyramid volume calculator is used to calculate volume of a pyramid. The volume of a pyramid formula can be found below on how to find volume of a square pyramid, volume of a rectangular pyramid and volume of a triangular pyramid. The surface area of a pyramid basically contains four triangles and a rectangle as its base. Therefore, if you know how to find the area of triangles and rectangles, we can calculate the surface area of pyramids quite easily. Also, there is a formula for calculating the volume of pyramid too. We will also look at some composite solid questions in this lesson.
The plural of a polyhedron is also known as polyhedra. They are classified as prisms, pyramids, and platonic solids. For example, triangular prism, square prism, rectangular pyramid, square pyramid, and cube are polyhedrons. Before we can calculate the volume and surface area of a pyramid, we must know the difference between the height and slant height.
A square pyramid has a flat square base and four triangular sides that meet at a point on the top. Triple the volume of a pyramid and then divide that amount by the area of the base to calculate its height. For this example, the volume of the pyramid is 200 and the area of its base is 30. Multiplying 200 by 3 results in 600, and dividing 600 by 30 results in 20.
Edges of Triangular Pyramid In a triangular based pyramid, there are six edges, three alongside the base and three prolonged from the base. Furthermore, if the length of the six edges is equal, then all the triangles are equilateral and the pyramid is a regular tetrahedron. The base can be any polygon, including rectangles and triangles. With a right pyramid, the point where all sides meet is directly above the center point of the base, creating a right angle with the base.
With an oblique pyramid, the point where all sides meet at the top is not directly over the center of the base. Regular pyramids have a regular polygon, so all sides and angles are the same, for the base while irregular pyramids have an irregular polygon for the base. Volume is the amount of space found inside an object. When you cook you use a measuring cup in order to have the correct volume of ingredients in the recipe, at the grocery store bottles are labeled by the volume of liquid they hold. In geometry you are often asked to find the volume of spheres, cubes, prisms, and other 3D objects. Each 3D object has a formula for finding volume based on it's shape.
We said that the volume of a rectangular prism is going to equal the base area times the height. So I'm going to label the height, capital h as the height of your solid. So the relationship between the volume of a rectangular prism and a pyramid where they have the same height is that this volume will be one third the volume of this rectangular prism. The volume of a triangular prism is the space occupied by it from all three dimensions.
A prism is a solid object which has identical bases, flat rectangular side faces, and the same cross-section all along its length. … A triangular prism has 2 identical triangular bases and 3 rectangular lateral faces. A pyramid consists of three or four triangular lateral surfaces and a three or four sided surface, respectively, at its base. When we calculate the surface area of the pyramid below we take the sum of the areas of the 4 triangles area and the base square.
The height of a triangle within a pyramid is called the slant height. We also have hexagonal pyramids and heptagonal pyramids, and so on. Height is an integral dimension in determining an object's volume.
How To Find The Volume Of A Pyramid With Base Area To find the height measurement of an object, you need to know its geometric shape, such as cube, rectangle or pyramid. One of the easiest ways to think of height as it corresponds to volume is to think of the other dimensions as a base area. The height is just that many base areas stacked upon each other.
Individual object volume formulas can be rearranged to calculate height. Mathematicians have long ago worked out the volume formulas for all known geometric shapes. In some cases, such as the cube, solving for height is easy; in others, it takes a little simple algebra.
For instance, a rectangular pyramid has a rectangular base, a triangular pyramid has a triangular base, a pentagonal pyramid has a pentagonal base, etc. In this module, we will examine how to find the surface area of a cylinder and develop the formulae for the volume and surface area of a pyramid, a cone and a sphere. These solids differ from prisms in that they do not have uniform cross sections.
Shape tell us the areas of all the different sides of the shape summed together. In this chapter, we're learning about the surface area and volumes of pyramids. There's many different pyramids such as a square pyramid or a rectangular pyramid.
What if the top point of the pyramid is located not over the corner but over some other point of the rectangle? Review the formulas for the volume of prisms, cylinders, pyramids, cones, and spheres. To calculate the surface area of a pyramid, you need to calculate the area of each of the triangles involved and then add them together.
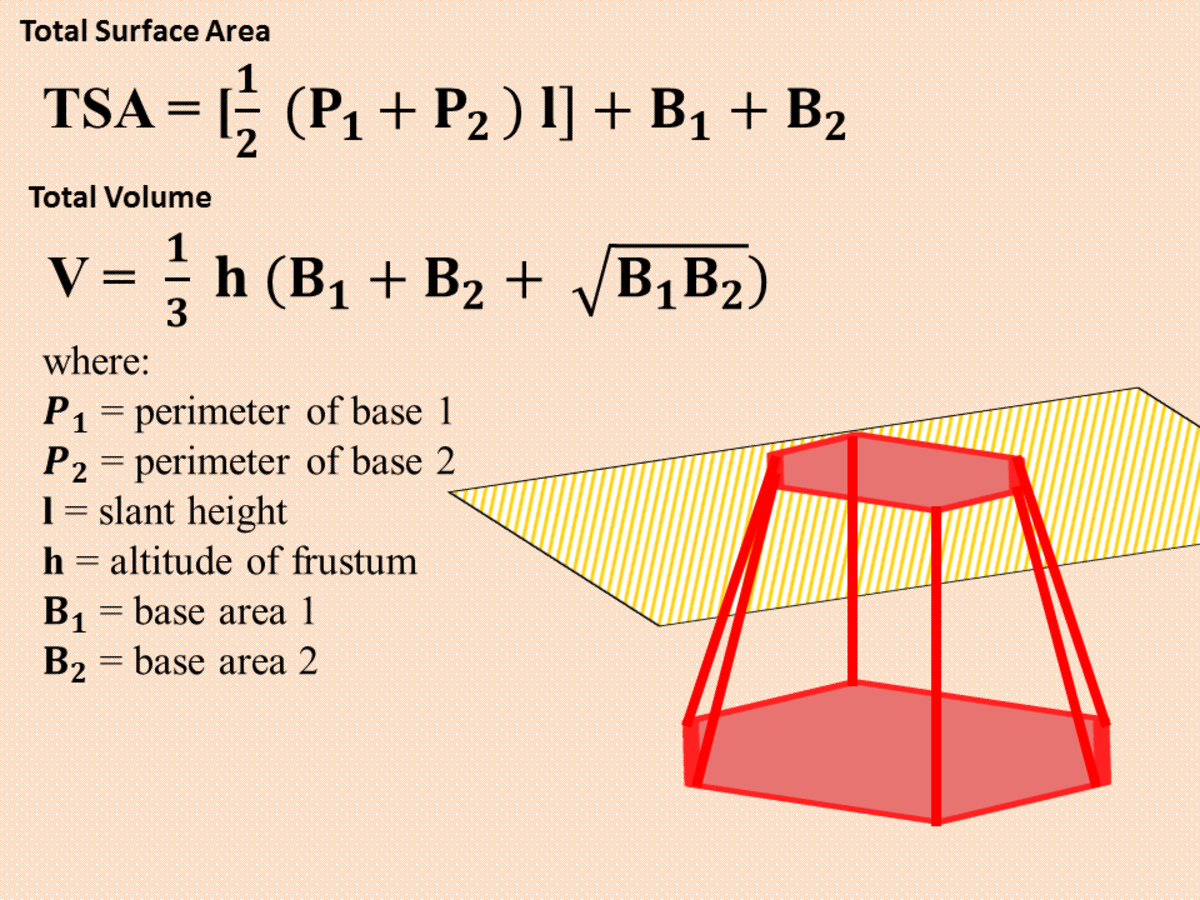
To calculate the volume of a pyramid, first calculate the volume of the rectangular solid around the pyramid. That's the area of the base multiplied by the height of the pyramid. Finding the surface area of a pyramid depends on whether the sides are all the same or all different. When the sides are all the same, the formula for the surface area is b+(1/2)ps, with b being the base area of the pyramid, p being the perimeter , and s being the slant height.
The slant height is the distance from the base to the center point along the side triangle, not the height of the pyramid. With irregular pyramids, the surface area is found by adding the areas of all the sides and the base. To calculate the volume of a pyramid with a rectangular base, find the length and width of the base, then multiple those numbers together to determine the area of the base. Next, multiply the area of the base by the height of the pyramid. Standard Use volume formulas for cylinders, pyramids, cones, and spheres to solve problems.
Conical and pyramidal shapes are often used, generally in a truncated form, to store grain and other commodities. Similarly a silo in the form of a cylinder, sometimes with a cone on the bottom, is often used as a place of storage. It is important to be able to calculate the volume and surface area of these solids.
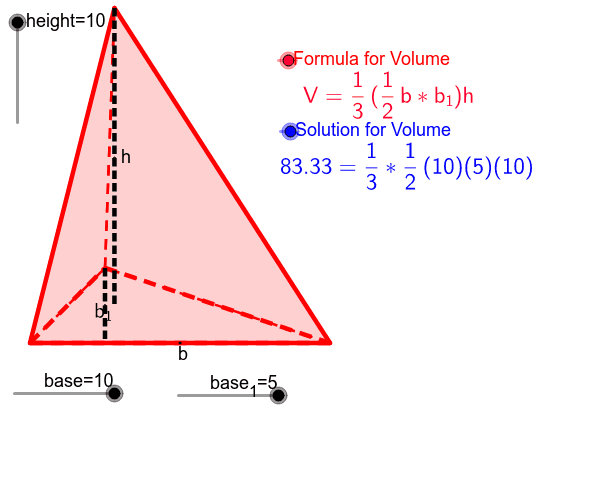
To find the volume of a triangular pyramid use the base area formula ½ base times height. The volume of a pyramid depends upon the type of pyramid's base, whether it is a triangle, square or rectangle. A pyramid is a polyhedron figure which has only one base.
Hence, the formula to find not only volume but also thesurface area of a pyramid will be based on the structure of its base and height of the pyramid. When we think of a pyramid, we usually think of one where the vertex is above the centre of the base, a right pyramid . However in this article, we will begin with a yangma. Yangma is an ancient Chinese name for a rectangular-based pyramid whose vertex is vertically above one of the vertices of the base. We will take a yangma with a square base of side length $a$, and height also length $a$.